티스토리 뷰
[※ 주의 ※] 아래를 이해하지 않고 이 글을 볼 경우, 이해가 되지 않는 부분이 있을 수 있습니다.
1. [Algorithm] 어떤 알고리즘이 더 빠르고 효율적인가? - 시간 복잡도 (3)
가장 "작은" 함수들끼리의 증가 속도를 비교하여 보자.
통상 사용되는 "작은" 함수들의 개형을 나타내면, 아래 차트와 같은 결과를 얻을 수 있다.
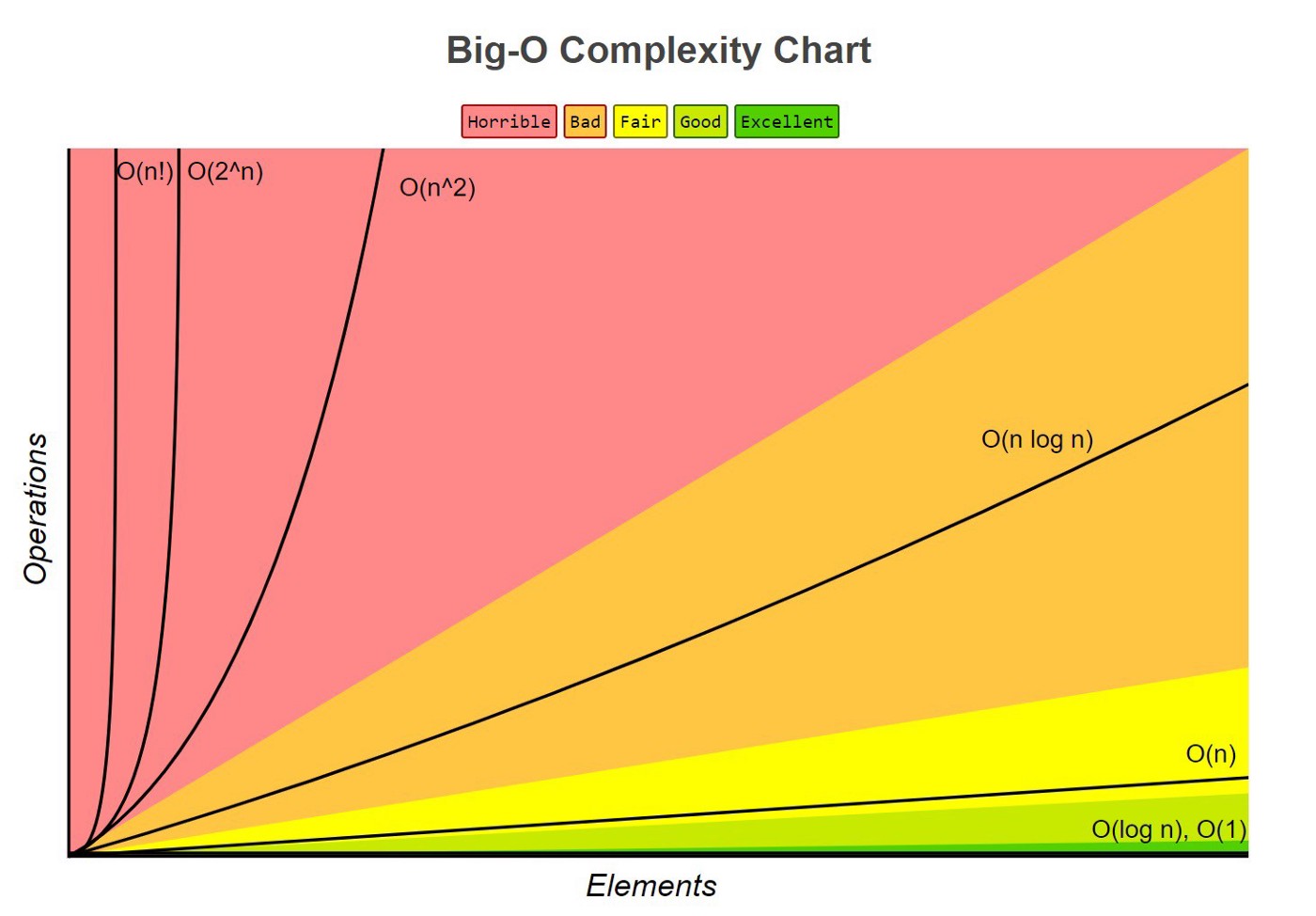
"작은" 함수들 ($1,\,n,\,\log n,\,n\log n,\,n^2,\,2^n,\,n!$)을 비교하였을 때 증가속도의 크기는 다음과 같이 쓸 수 있다.
$$\large O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(2^n) < O(n!) < \cdots$$
따라서, 만약 여러 알고리즘이 중첩된다면 더 오른쪽에 있는 알고리즘의 속도를 고려하면 된다.
이제, 각 알고리즘 별 예시를 생각하여보자.
1. 상수 시간 알고리즘 $O(1)$
상수 시간 알고리즘은 하나의 연산 혹은 아주 작은 연산으로 알고리즘을 표현할 수 있으며, 입력의 크기에 영향을 받지 않는 알고리즘이다.
상수 시간 알고리즘의 예시는 다음과 같다.
1 2 3 4 5 6 7 8 | // Example of O(1) // 1. print cout << 2; // 2. basic operation int a = 1 + 2; int b = 3 / 4; int c = nums[0]; | cs |
위의 알고리즘들은 어떤 입력이 들어와도, 항상 같은 연산 수행 횟수를 수행한다. 다른 말로, 매우 빠른 시간 내에 수행할 수 있는 알고리즘이라고 생각하면 된다.
PS. 컴퓨터 내부에서의 기본 산술 연산(덧셈, 뺄셈, 곱셈, 나눗셈) 구현은 다항 시간 알고리즘 $O(n^k)$ 으로 구현되어 있다. 다만, 입력의 크기에는 영향을 받지 않기에 상수 시간 알고리즘으로 분류하였다.
2. 로그 시간 알고리즘 $O(\log n)$
로그 시간 알고리즘은 연산의 수행 횟수 및 총 수행 시간이 입력의 로그함수에 비례하며, 이는 $n$개의 데이터 모두 탐색하지 않아도 된다는 의미이다. (굉장히 중요한 말이다.)
로그 시간 알고리즘도 상수 시간 알고리즘 만큼이나 빠르게 작동한다.
맨 위의 [그림 1]에서 볼 수 있듯이, 아무리 $n$의 크기가 증가하여도 $O(\log n)$의 증가 속도는 매우 작다는 것을 확인할 수 있다. $n$이 충분히 작을 경우 로그 시간 알고리즘의 속도는 상수 시간 알고리즘의 속도와 매우 유사하다.
로그 시간 알고리즘의 예시는 다음과 같다.
만약, 1부터 10,000,000까지의 수 중에서 100,000개 들어가있는, 정렬된 container에서 원하는 값을 찾는다고 할 때, 다음과 같이 이분 탐색(Binary Search)을 활용하면 로그 시간 알고리즘 내에 찾을 수 있다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | // Example of O(log n) // 1. binary search int binary_search(vector<int> nums, int target) { int nums_length = nums.size(); int left = 0, right = nums_length-1; while (left <= right) { int mid = (left + right) / 2; if (target == nums[mid]) { return mid; } else if (target < nums[mid]) { right = mid - 1; } else { left = mid + 1; } } // cannot find target return -1; } | cs |
이분 탐색 알고리즘 글에서 자세히 설명하겠지만, 만약 중간값이 원하는 값보다 크다면, 중간값보다 오른쪽에 있는 값들을 모두 탐색하지 않고, 새로운 탐색범위를 지정하는 방법을 통해 $n$개의 데이터 모두 탐색하지 않는 모습을 확인할 수 있다.
3. 선형 시간 알고리즘 $O(n)$
선형 시간 알고리즘은 우리가 보통 모든 데이터를 한 번씩 들여다 보는 알고리즘으로, 입력의 크기에 비례하여 수행 시간 및 연산 수행 횟수가 증가하는 알고리즘이다.
로그/상수 시간 알고리즘보단 느리지만 그래도 꽤 빠른 알고리즘이다.
하나의 예시를 들자면 1부터 10,000,000까지의 수 중에서 100,000개 들어가있는 container에서 원하는 값을 찾는다고 할 때, 하나씩 값을 비교하며 값을 찾는 선형 검색(Linear Search) 알고리즘은 선형 시간 알고리즘의 시간 복잡도를 지닌다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | // Example of O(n) // 1. linear search int linear_search(vector<int> nums, int target) { int nums_length = nums.size(); for (int i = 0; i < nums_length; i++) { if (nums[i] == target) { return i; } } // cannot find target return -1; } | cs |
데이터를 하나씩 확인하기 때문에, 최악의 경우 배열 전체를 탐색할 수 있다. (원하는 값이 배열 마지막에 있는 경우)
따라서, 선형 검색 알고리즘은 배열 전체의 크기, 즉 $n$에 따라 비례하여 증가한다고 할 수 있다.
4. 선형 로그 시간 알고리즘 $O(n\log n)$
선형 로그 시간은 알고리즘의 수행 시간이 선형과 로그 시간의 중첩의 속도를 가진 알고리즘으로, 모든 데이터를 한 번씩 들여다보지만, 특정 조건 하에 한 번 이상 들여다볼 수 있는 알고리즘의 의미를 지닌다.
특히, 분할-정복 알고리즘(Divide-Conquer Algorithm)에서 자주 보이는 알고리즘 수행시간으로, 선형 시간 알고리즘보단 느리지만 다항 시간 알고리즘보다는 빠르다. 아직은 사용하기 괜찮은 수행 시간으로 분류된다.
선형 로그 시간 알고리즘의 예시로 다음과 같은 것들이 있다.
- 합병 정렬 (Merge Sort)
- 퀵 정렬 (Quick Sort)
- 힙 정렬 (Heap Sort)
- 고속 푸리에 변환 (Fast Fourier Transform) => 빠른 큰 수 곱셈 알고리즘
각각의 알고리즘에 대한 설명은 별도의 포스팅으로 만나도록 하겠다.
5. 2차 시간 알고리즘 $O(n^2)$
2차 시간 알고리즘, 혹은 $n$제곱 알고리즘은 모든 데이터를 평균 두 번보는 알고리즘으로, 입력의 크기의 제곱에 비례하여 수행 시간 및 연산 횟수가 증가하는 알고리즘이다.
2차 시간 알고리즘은 입력의 크기의 제곱에 따라 수행 시간이 결정되기에, 입력의 크기가 크다면 수행 시간이 슬슬 부담스러운 시간이다. 다만, 너무 크지만 않으면 "쓸만한" 알고리즘 정도 되겠다.
2차 시간 알고리즘은 보통 선형 시간 알고리즘 두 번이 중첩된 경우가 많다.
2차 시간 알고리즘의 예시로 다음과 같은 것들이 있다.
- 버블 정렬 (Bubble Sort)
- 삽입 정렬 (Insertion Sort)
- 선택 정렬 (Selection Sort)
각각의 알고리즘에 대한 설명은 별도의 포스팅으로 만나도록 하겠다.
6. 지수 시간 알고리즘 $O(2^n)$
지수 시간 알고리즘은 모든 데이터를 지수 함수에 비례하여 알고리즘으로 어느 정도 큰 $n$이 입력으로 들어오면 연산 횟수가 급격하게 증가하는 알고리즘이다.
지수 시간 알고리즘은 대부분 알고리즘의 로직을 개선해야 실제 사용 가능하며, $n$이 100,000을 넘으면 컴퓨터가 연산을 포기하거나 매우 오랜 시간이 걸린다.
지수 시간 알고리즘을 활용하는 예시로는 재귀를 이용한 피보나치 수열의 값 구하기, 혹은 브루트 포스 알고리즘 정도 되겠다.
7. 팩토리얼 시간 알고리즘 $O(n!)$
팩토리얼 시간 알고리즘은 모든 데이터를 팩토리얼 함수에 비례하여 알고리즘으로, 지수 시간 알고리즘보다도 비효율적인 알고리즘이다.
팩토리얼 시간 알고리즘도 알고리즘의 로직을 개선해야 실제 사용가능하며, $n$이 1,000만 넘어도 컴퓨터로 연산하기 거의 불가능한 시간 복잡도를 지닌 알고리즘이다.
팩토리얼 알고리즘을 활용하는 예시는 브루트포스 알고리즘 정도 되겠다. 이 이상의 알고리즘은 논의하는 것이 무의미하기에 생략하겠다.
그럼, 실제 코드에선 어떻게 시간복잡도를 예상해야 할까? 이번 글을 이해하였으면 다음 글로 넘어가 보자.
'Algorithm' 카테고리의 다른 글
| [Algorithm] 어떤 알고리즘이 더 빠르고 효율적인가? - 시간복잡도 (5) (2) | 2022.04.17 |
|---|---|
| [Algorithm] 어떤 알고리즘이 더 빠르고 효율적인가? - 시간복잡도 (3) (0) | 2022.04.13 |
| [Algorithm] 어떤 알고리즘이 더 빠르고 효율적인가? - 시간복잡도 (2) (0) | 2022.04.13 |
| [Algorithm] 어떤 알고리즘이 더 빠르고 효율적인가? - 시간복잡도 (1) (0) | 2022.04.13 |
- Total
- Today
- Yesterday
- 제어문
- 백준
- 구현
- equal
- for
- 시간복잡도
- 문자열
- BRONZE
- Proactor
- CSAPP
- Python
- JS
- 함수
- Max
- effective async
- 알고리즘
- C++
- GDSC
- docker
- 헤더
- Network
- MIN
- 사칙연산
- bomblab
- BOJ
- C
- 프로그래밍
- react
- 수학
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
